Chapter 1
Compressible Flow
Compressible Flow
Overview
This first chapter gives an overview of the field of compressible flow. In the first sections important milestones in the compressible flow history are presented. Concepts and parameters relevant for compressible flows are introduced and discussed. A short review of thermodynamics is given at the end of the chapter.
Online Flow Calculator
Sections of the online flow calculator for compressible flow problems CFLOW related to this chapter:
- Section 1: Gas Relations
Chapter Roadmap
Sections
1.2 Definition of Compressible Flow
This chapter discusses the difference between compressible and incompressible flow. The concept compressibility is defined and discussed.
Compressibility is defined as the relative change in specific volume related to a change in pressure
$$\tau=-\dfrac{1}{\nu}\dfrac{\partial \nu}{\partial p}$$This definition must be complemented with information about the process by which the pressure is changed. Two processes are introduced, namely the constant-temperature process and the adiabatic (no heat exchange) process.
Flows where changes in density (or specific volume) are too large to be neglected should be treated as compressible. Typically this means that the relative change in density is greater than 5% (\(\Delta \rho/\rho > 0.05\)).
1.3 Flow Regimes
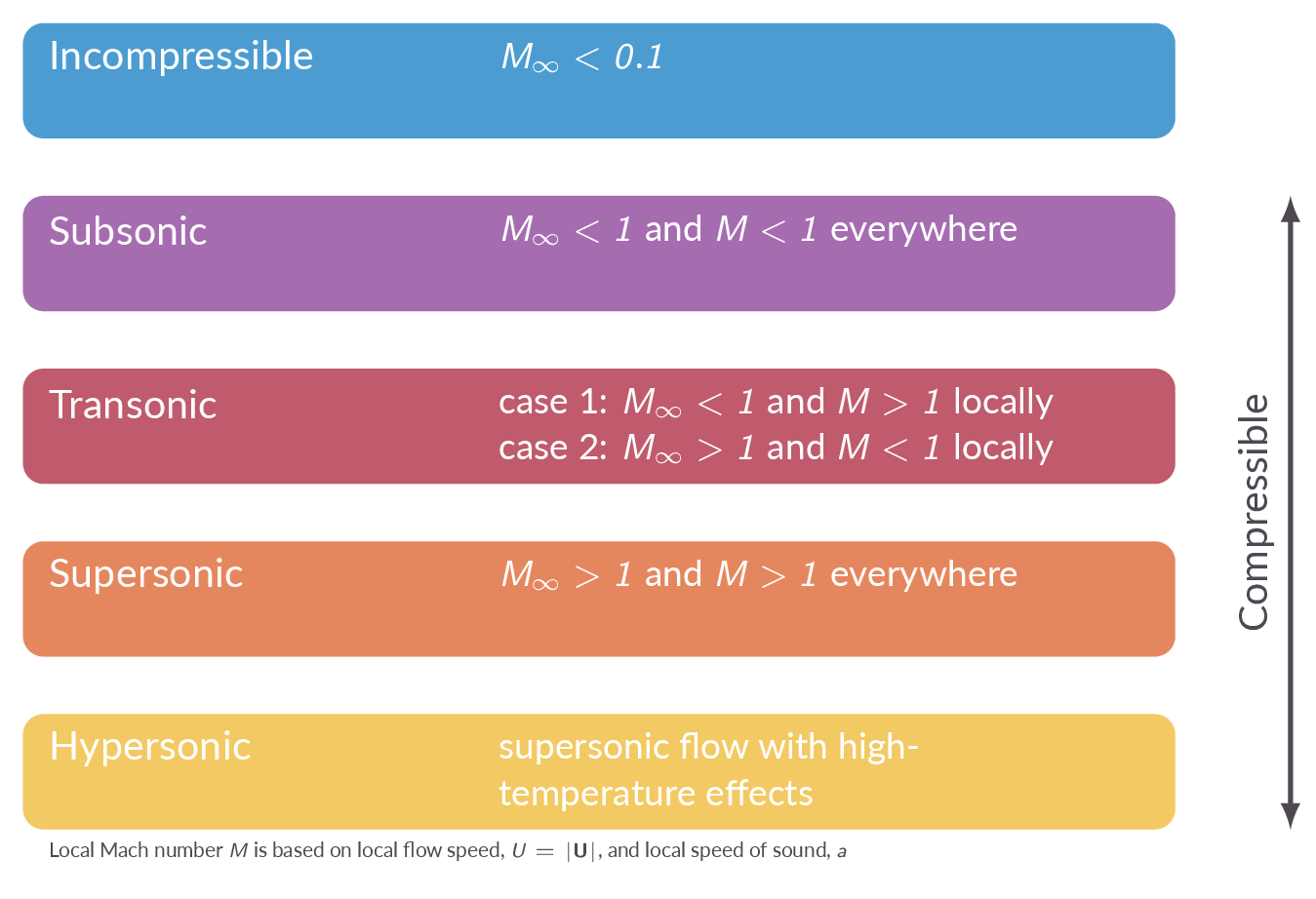
The free stream and local Mach numbers are defined as \(M_\infty=V_\infty/a_\infty\) and \(M=V/a\), respectively. The Mach number is used to define different regimes of compressible flows (subsonic, transonics, supersonic, hypersonic). The concept inviscid flows is introduced.
1.4 A Brief Review of Thermodynamics
This chapter gives, as the title hints, a short review of thermodynamics. Concepts important for compressible flows are introduced:
- perfect gas
- equation of state (ideal gas law) \(p=\rho RT\)
- internal energy \(e\)
- enthalpy \(h=e+p/\rho\)
- thermally perfect gas
- callorically perfect gas
- specific heat
$$C_v=\left(\frac{\partial e}{\partial T}\right)_v$$
$$C_p-C_v=R$$
$$\gamma=\frac{C_p}{C_v}$$
$$C_p=\frac{\gamma R}{\gamma-1}$$
$$C_v=\frac{R}{\gamma-1}$$
In a thermally perfect gas energy and enthalpy are functions of temperature. A calorically perfect gas is a subset of thermally perfect gases where energy and enthalpy are linear functions of temperature (the specific heats are constants). The calorically perfect gas assumption applies for temperatures in the range 100 K to 600 K while the thermally perfect gas assumption applies up to about 2500 K.
The first law of thermodynamics is introduced and described.
$$\delta q + \delta w =de$$where \(de\) is the change in internal energy of a system (a identifiable set of molecules or a fixed mass), \(\delta q\) is heat added to the system from its surroundings, and \(\delta w\) is work done by the system on its surroundings. The heat addition and fluid work are process dependent.
Three type of processes are introduced:
- adiabatic (no heat exchange)
- reverisible (no irreversible losses introduced)
- isentropic (adiabatic and reversible)
The concept of entropy is introduced and discussed in the framework of the second law of thermodynamics. The first and second laws of thermodynamics combined gives
$$ds= C_p\dfrac{dT}{T}-R\dfrac{dp}{p}$$Integrated between two stations 1 and 2 the relation above becomes
$$s_2-s_1=\int_1^2C_p\dfrac{dT}{T}-R\ln\left(\dfrac{p_2}{p_1}\right)$$If the gas is calorically perfect (constant specific heats) we get
$$s_2-s_1=C_p\ln\left(\dfrac{T_2}{T_1}\right)-R\ln\left(\dfrac{p_2}{p_1}\right)$$Finally, for an isentropic process (\(s_2=s_1\)), this leads to the isentropic relations for calorically perfect gases, which will prove to be very useful throughout the rest of the book.
$$\frac{p_2}{p_1}=\left(\frac{\rho_2}{\rho_1}\right)^{\gamma}=\left(\frac{T_2}{T_1}\right)^{\gamma/(\gamma-1)}$$Aerodynamic Forces on a Body
This section describes how forces on a body immersed in a fluid flow can be calculated. As an example, a formula for the evaluation of aerodynamic forces on a wing is derived and in conjunction with that the force components lift and drag are introduced.
Study Guide
The questions below are intended as a "study guide" and may be helpful when reading the text book.
- How are the compressibility factors \(\tau_T\) and \(\tau_S\) defined?
- For a given flow, how can we determine if compressibility effects are important?
- Use the Bernoulli equation (even though it's not valid for compressible flows) to obtain an estimate of the Mach number for which compressible effects becomes significant and must be considered.
- What are the criteria for the classifications subsonic/transsonic/supersonic/hypersonic flow?
- What is a perfect gas and what relation between pressure, density, temperature may be used for such a gas?
- What do we mean by thermally perfect gas and calorically perfect gas respectively?
- When can air be regarded as a calorically perfect gas?
- Define \(C_p\), \(C_v\), and \(\gamma\)
- In the first law of thermodynamics, how is a {\bf{system}} defined?
- What is a reversible process?
- What is an adiabatic process?
- What are the criteria for an isentropic process, i.e. what conditions must be satisfied for a steady-state compressible flow to be isentropic?
- How do we define entropy for a gas?
- What does the second law of thermodynamics say about entropy?
- Derive the isentropic relations for calorically perfect gases starting from the entropy equation.
- In Formulas, Tables & Graphs, check all thermodynamics formulas for thermally perfect gas and calorically perfect gas on the first three pages. You should be familiar with these formulas and know when/how to apply them.
