Case 7
Supersonic flow over a gradual 2D compression ramp
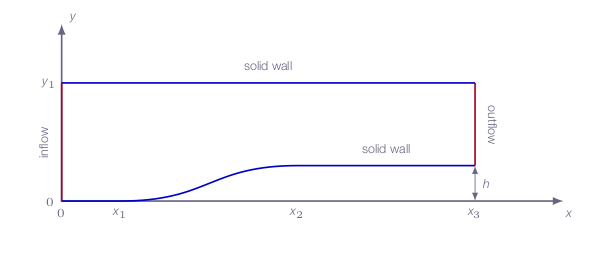
 This problem includes inviscid compressible flow in two space dimensions. The geometric dimensions of the computational domain is given in the figure below and the problem consists of computing the 2D unsteady flow in a gradual compression ramp according to specifications below. The flow will include feautures such as compression regions, shocks, and expansion regions. A supersonic flow is imposed at the inlet boundary.
This problem includes inviscid compressible flow in two space dimensions. The geometric dimensions of the computational domain is given in the figure below and the problem consists of computing the 2D unsteady flow in a gradual compression ramp according to specifications below. The flow will include feautures such as compression regions, shocks, and expansion regions. A supersonic flow is imposed at the inlet boundary.
Literature review
Suggested search topics
- Oblique shock
- Prandtl-Meyer expansion
- Shock-expansion theory
- Slip line
- Compression ramp
- Shock reflection
- Mach reflection
Specifications
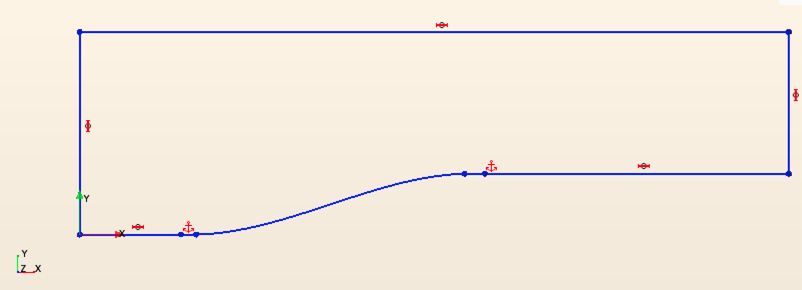
The smooth ramp section starts at \((x,y)=(x1,0.0)\) and reaches \(y=h\) at the axial coordinate \(x=x_2\). For the lower wall and axial coordinates greater than \(x_2\), \(y\) is constant (\(y=h\)).
x1 = 1.0 m
x2 = 4.0 m
x3 = 7.0 m
y1 = 2.0 m
h = 0.6 m
For an inlet Mach number of 2.0, the inlet and outlet flow conditions are as follows:
| inlet | |
| \(\rho\) | 0.267124 \(kg/m^3\) |
| \(p\) | 12780 \(Pa\) |
| \(u\) | 517.61 \(m/s\) |
| outlet | |
| \(\rho\) | 0.4045 \(kg/m^3\) |
| \(p\) | 22840 \(Pa\) |
| \(u\) | 455.481 \(m/s\) |
Task 1
Do an inviscid simulation for the smooth compression ramp as specified above
Task 2
Investigate the effect of viscosity for the compression ramp flow by running a viscous simulation using the Spallart-Almaras turbulence model.
Expected results and presentation
The flow field will contain compression regions, oblique shocks, and expansion fans. Although contour plots should be used for the visualization of these flow features it might be difficult to do a qualitative comparison of different simulations (simulations made using different meshes and numerical settings) and analytical results. Therefore, when comparing shock strength and location of flow features, it is recommended to extract data along axial lines at different \(y\) coordinates and compare the data in terms of \(xy\)-plots.
Grid generation guidelines
There should not be any large jump in cell sizes anywhere. The changes in cell size must be smooth otherwise you might run into problems with convergence.
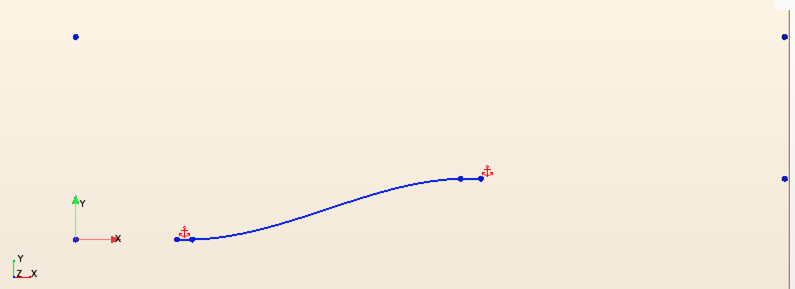
The smooth ramp contour can be generated using the spline functionality in the STAR-CCM+ sketch tool. Start by making two points using the Create point tool.

Adjust the coordinates according to the specifications for \(x_1\) and \(x_2\) above. Then right click on each of the two points and click Apply Fixation Constraint. This will make sure that the spline generation tool does not modify the location of these coordinates later.

Now, use the Create Spline tool to generate the gradual ramp.
Select the \(x_1\) coordinate as the first point on the spline curve, then select two control points between the \(x_1\) and \(x_2\) (these points can be moved later). Select the \(x_2\) coordinate as the end point pf the spline curve. Press esc on your keyboard to exit the spline tool. Move the two control points such that the ramp looks smooth.
Now, connect all other corner points with lines and the sketch is done.
CFD guidelines
Some general guidelines for the simulation:
- Don't forget to set the reference pressure to zero:
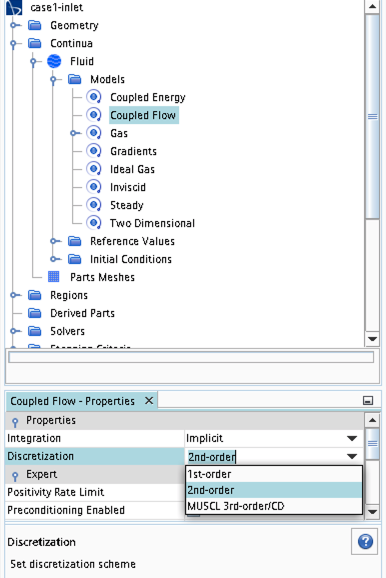
Continua -> Fluid -> Reference Values -> Reference Pressure- In your project, you should investigate the performance of different numerical schemes. The numerical scheme is modified under
Continua -> Fluid -> Models -> Coupled Flow. Note, in case you have not renamed the physics entry underContinua, the default name isPhysics 1.
- Some of the cases, or at least some of the operation conditions for some cases, will have convergence problems due to flow instabilities. In case you get that type of solver behavior, try to find another convergence criterion by for example measuring forces or massflow. You may also consider updating the mesh as it is crucial to resolve important flow features to reach convergence.
- Some of the cases should be simulated using a viscous solver. Choose
Turbulentinstead ofInviscidwhen you select models and then select an appropriate turbulence model.

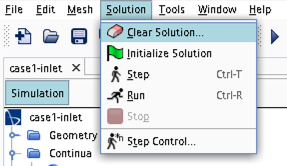
- In case you would like to start your simulation from scratch, the flow field can be reset as indicated in the picture below (don't forget to initialize the flow field after the reset).
- Time stepping approach (implicit/explicit) is selected under
Continua -> Fluid -> Models -> Coupled Flow
- CFL number and other solver settings are found under
Solver -> Coupled Implicit(orSolver -> Coupled Explicit)