Chapter 4
Oblique Shocks and Expansion Waves
Oblique Shocks and Expansion Waves
Overview
In real life supersonic flow applications, normal shocks as the ones studied in Chapter 3 appear in very specific situations only. The situation will rather be that a complex shock pattern built up of combinations of oblique shocks, expansion waves and slip lines will be formed. The nature and geometry of the generated shocks formed around an object depends on flow Mach number and the geometry of the object.
Online Flow Calculator
Sections of the online flow calculator for compressible flow problems CFLOW related to this chapter:
- Section 1: Gas Relations
- Section 2: Total Flow Properties
- Section 3: Normal Shock Relations
- Section 6: Oblique Shock Relations
- Section 7: Expansion Waves
Chapter Roadmap
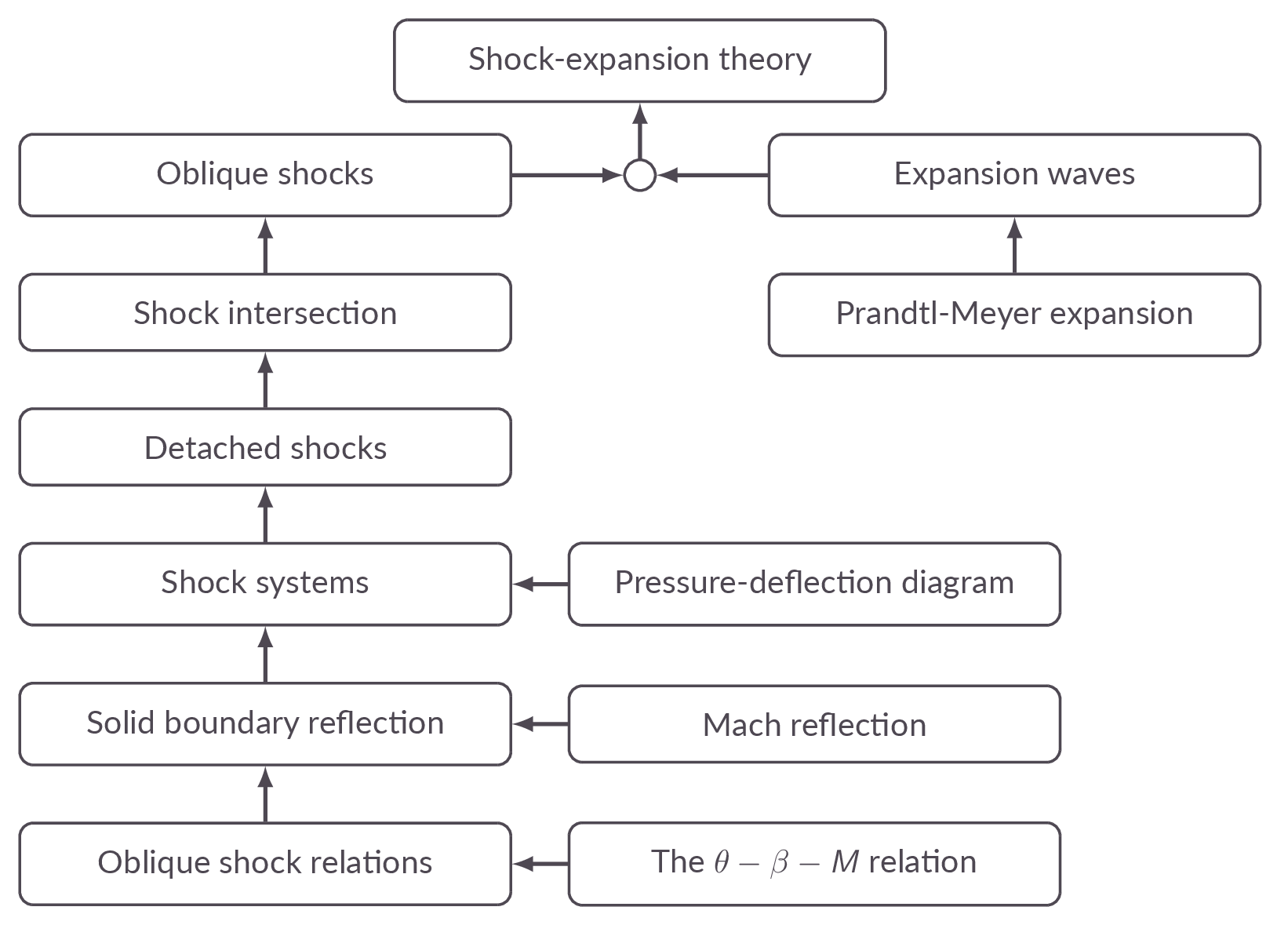
Sections
4.2 Source of Oblique Waves
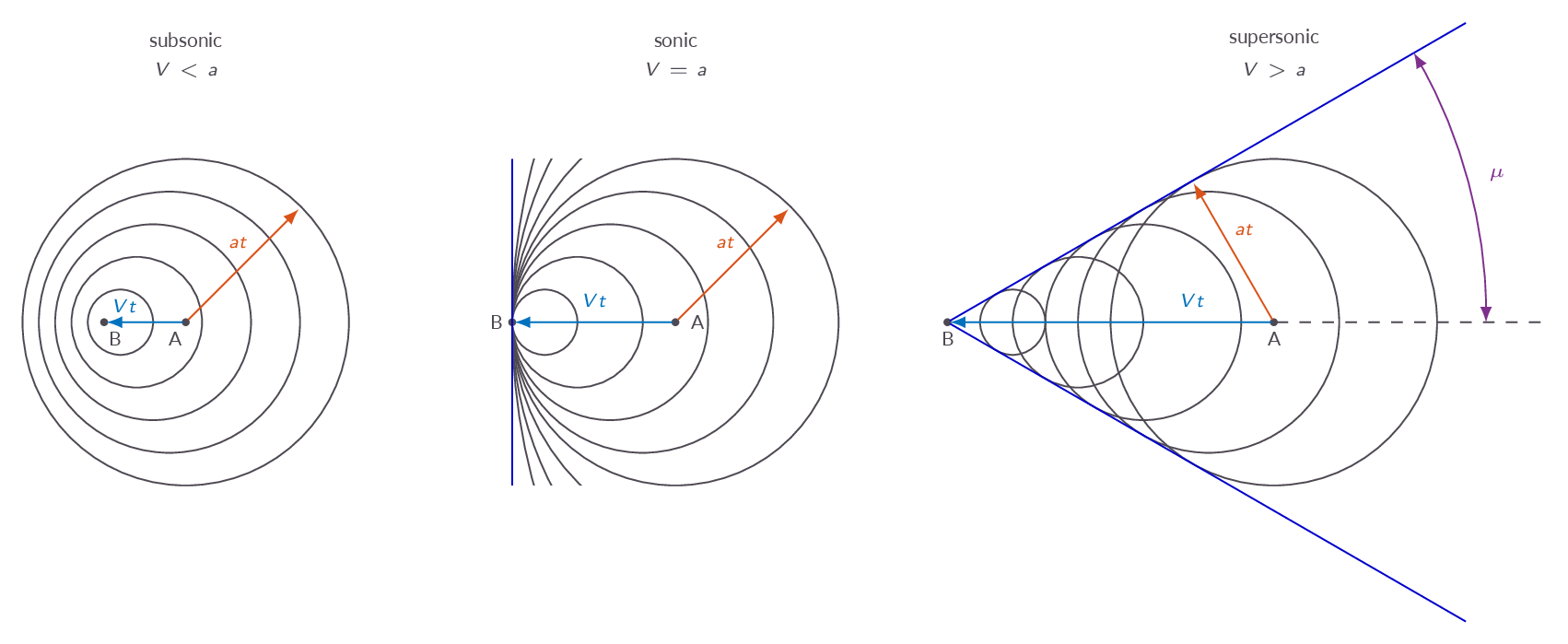
Oblique waves are disturbances that propagate by molecular collision at the speed of sound. Oblique waves may eventually coalesce and form oblique shocks or spread out to form an expansion wave.
The formation of Mach waves is described. The Mach wave angle is dependent on the free stream Mach number. The relation between the free stream Mach number and the Mach angle is illustrated in Figure 1 below.
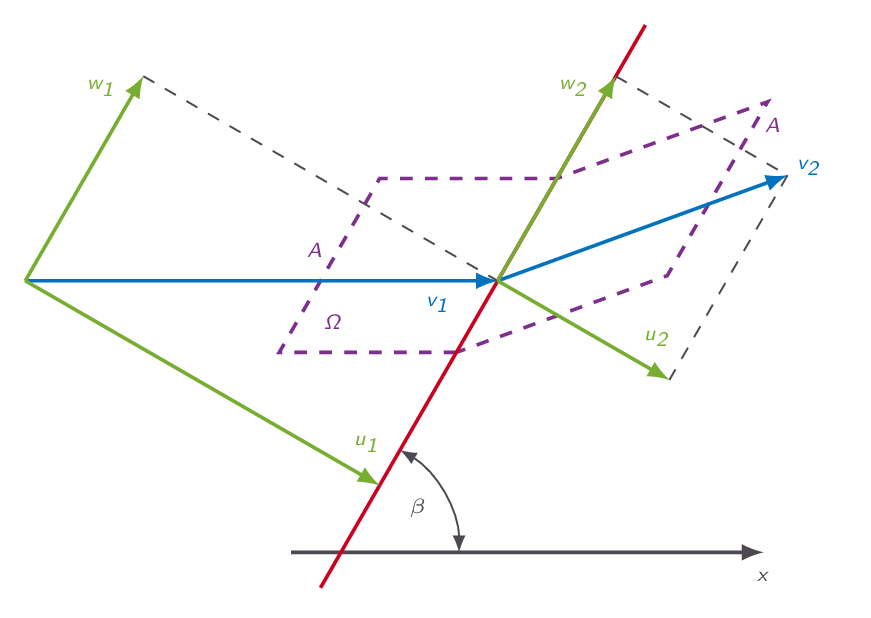
4.3 Oblique Shock Relations
The governing equations for an oblique shock are derived and, by coordinate transformation, it turns out that we can use most of the relations obtained for normal shocks in the shock-normal direction. Deriving the governing equations in the shock-normal direction and the direction along the oblique shock it is shown that the velocity in the direction along the shock is preserved over the shock.
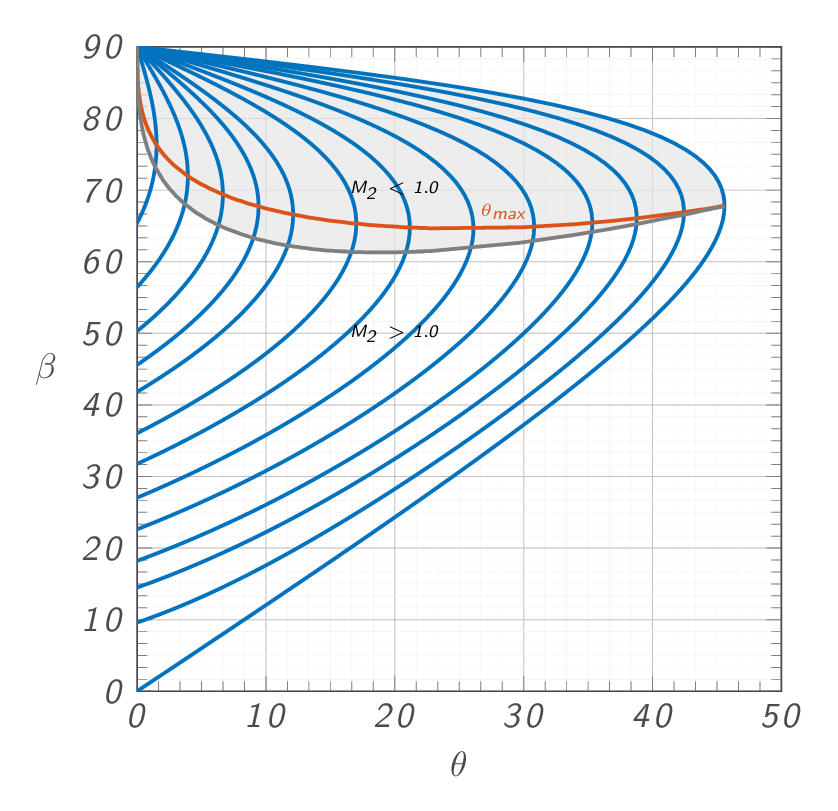
The \(\theta-\beta-M\)-relation is derived, which proves to be very important in the investigation of oblique shocks. The expression relates the free stream Mach number \(M\), the deflection angle \(\theta\), and the oblique shock angle \(\beta\). From the relation, it is obvious that each situation has two possible solutions one with a lower \(\beta\) angle that is referred to as the weak solution and one with a larger angle \(\beta\) that is referred to as the strong solution. In nature, the weak solution is preferred over the strong solution due to less losses. However, in some cases the strong solution may be the only solution possible due to downstream flow conditions.
4.4 Supersonic Flows Over Wedges and Cones
The generation of oblique shocks is illustrated by the examples of flow over wedges (two-dimensional flow) and cones (three-dimensional flow). It is shown how the oblique shock relations can be used to calculate the flow properties on the downstream side of an oblique shock given the free stream Mach number and the cone angle (the deflection angle).
4.5 Shock Polar
The shock polar constitutes a graphical tool that can be used to analyze and understand a oblique shock situation.
4.6 Regular Reflection from a Solid Boundary
What happens when an oblique shock reaches a wall? Will the shock reflect and, in case it does, how will it reflect?
This section gives examples where there is a need for another oblique shock to be generated at the point where a first oblique shock reaches a wall in a channel configuration in order to deflect the flow such that it is aligned with the downstream wall. Since the incoming Mach number will not be the same, the angle of the oblique shocks will be different even if the deflection angle is the same. This means that the oblique shock is not specularly deflected.
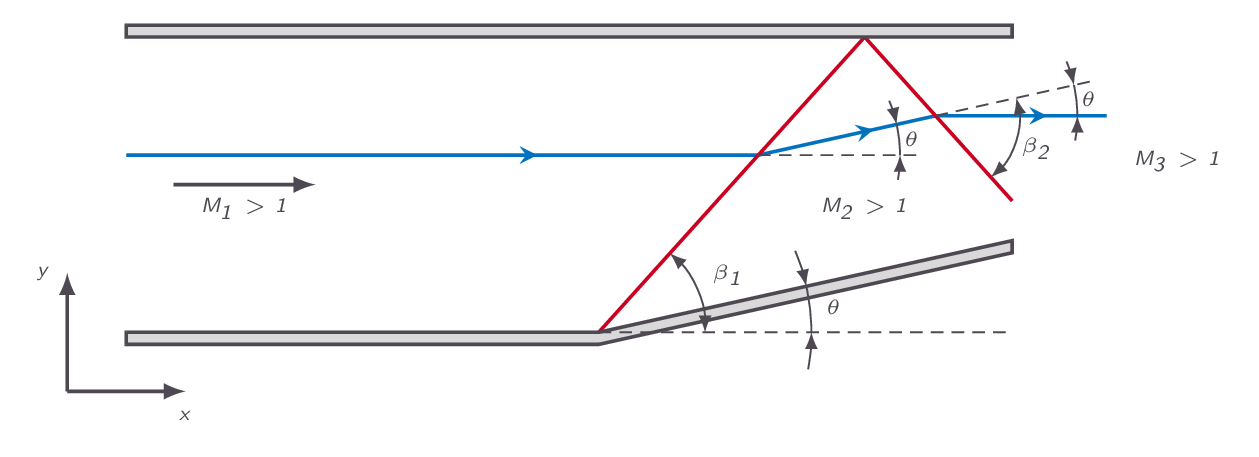
4.7 Comment on Flow Through Multiple Shock Systems
As oblique shocks generates less losses than normal shocks, a system of consecutive oblique shocks is, if possible, a solution preferred by nature (and engineers) over a single normal shock at all times. In some situations, however, no oblique shock solutions exists and thus a normal shock is the only alternative.
4.8 Pressure-Deflection Diagrams
The pressure-deflection diagram is yet another graphical tool used to analyze systems of shocks. In this section it is illustrated how a pressure-deflection diagram can be used to visualize the shock reflection at solid boundaries discussed in the previous section.
4.9 Intersection of Shocks of Opposite Families
More complex examples involving oblique shocks are introduced. What happens when left and right running shocks intersects?
The slip line concept is introduced. A slip line is a discontinuity in flow and thermodynamic quantities over which pressure and flow angle are continuous. A slip line can appear between two flow regions with the same flow direction where the fluid in the two regions has passed different shock systems on its way there. Passing different shock systems implies that the losses introduced are different and so is the flow Mach number, temperature, density.
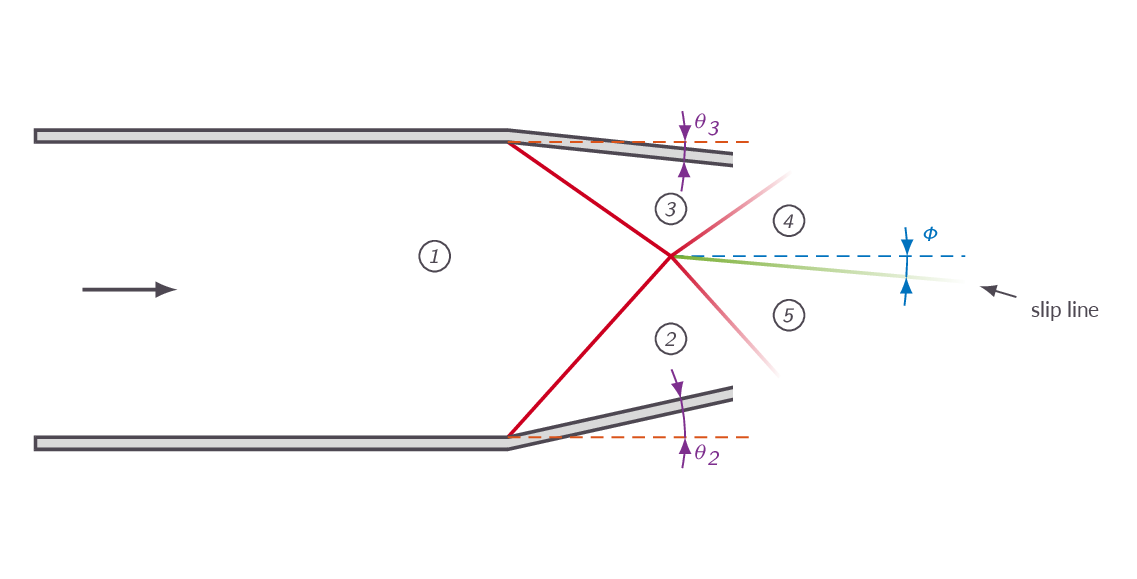
Again the pressure-deflection diagram is used to illustrate the shock system graphically.
4.10 Intersection of Shocks of the Same Families
It is shown that Mach waves generated at the upstream or downstream side of an oblique shock will intersect with the shock at some point. Intersection of shocks of the same family is also discussed.
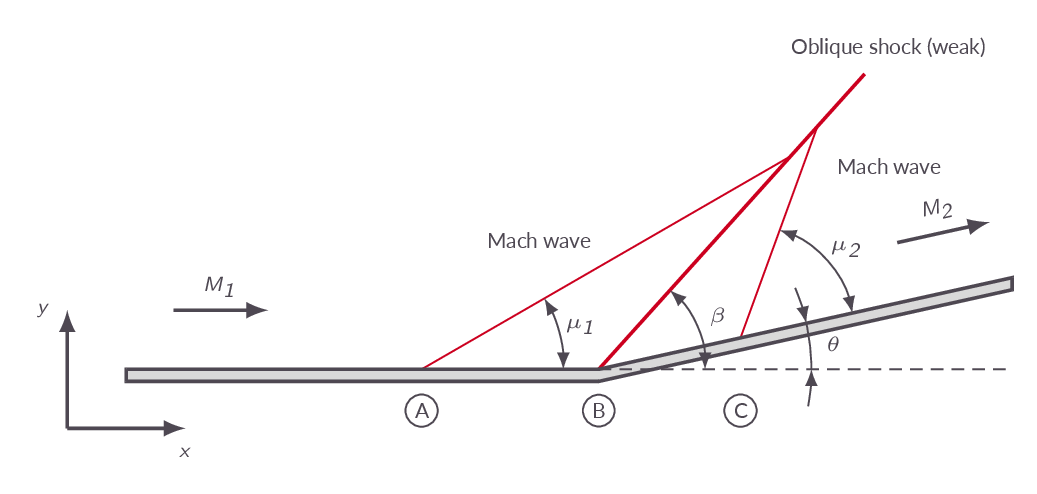
4.11 Mach Reflection
Regular shock reflection as discussed in section 4.6 is possible only if the \(\theta-\beta-M\)-relation has a solution for the given Mach number and deflection angle. If that is not the case, we will instead get a Mach reflection at the solid wall. This means that a normal shock is formed at the wall that away from the wall bends of to match the angle of the oblique shock. To be able to analyze the flow in a Mach reflection case we will need to use CFD.
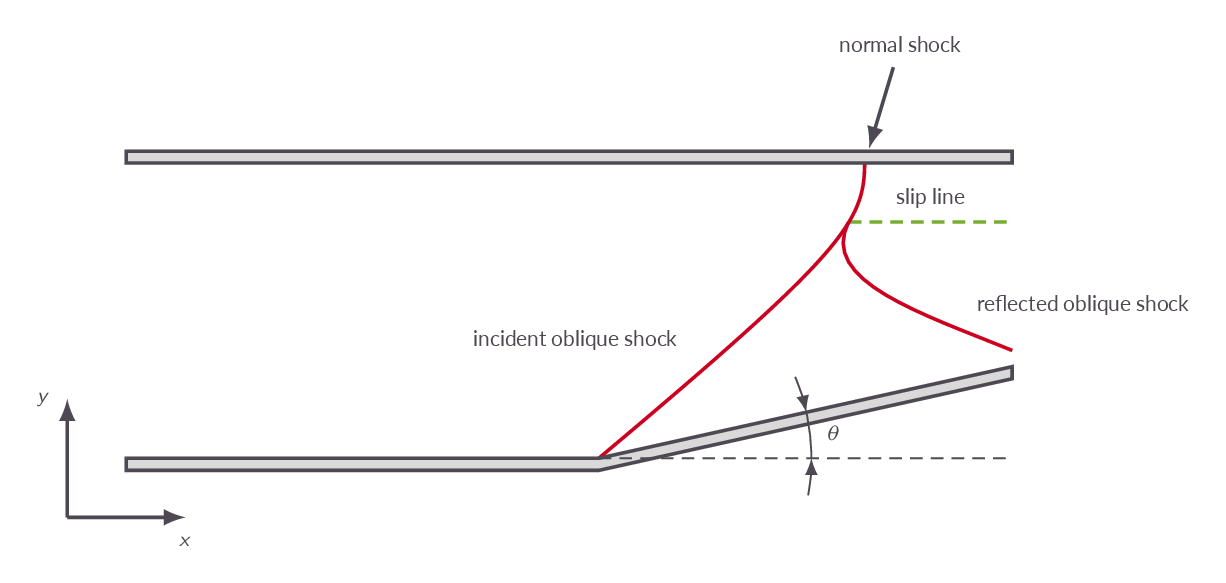
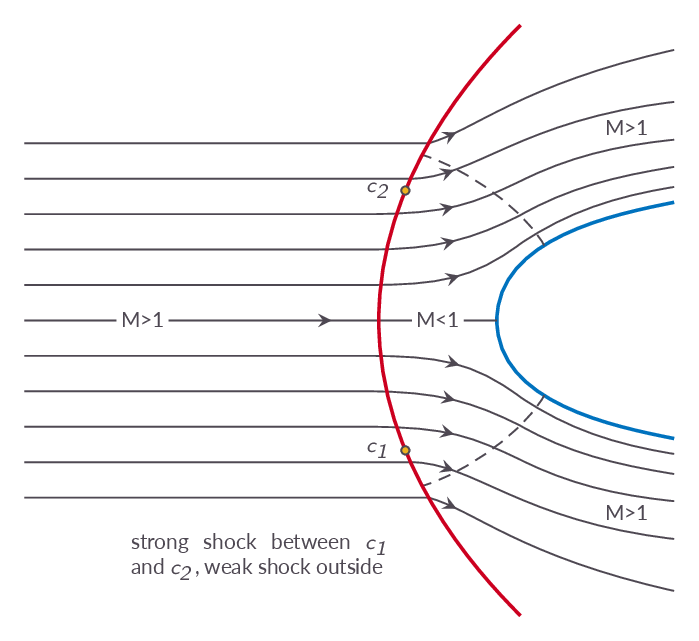
4.12 Detached Shock Wave in Front of a Blunt Body
In front of a blunt body, generation of oblique shocks is not possible and instead we will get a detached bow shock. In front of the object, the detached shock is normal generating a region of subsonic flow in front of the object. Away from the object, the shock bends of and becomes an oblique shock, which means that the flow behind the shock may very well be supersonic downstream of the shock. This gives us a transonic flow situation, i.e. a supersonic flow field with small regions of subsonic flow.
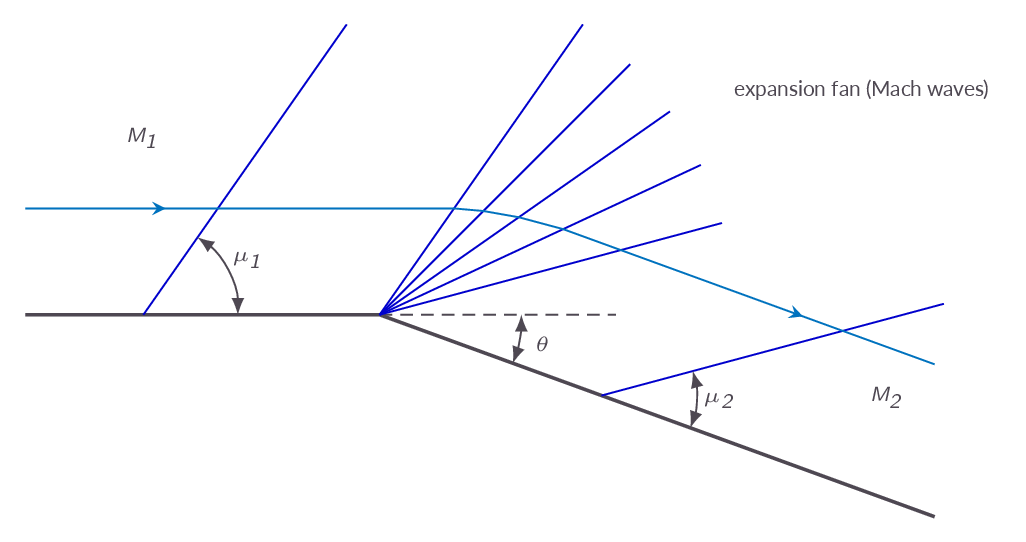
4.14 Prandtl-Meyer Expansion Waves
Expansion waves are in many ways the antithesis of shock waves. They arise when a supersonic flow is turned away from itself. An expansion region is built up of an infinite number of weak Mach waves. Since each Mach wave is isentropic the entire expansion region is isentropic, which means that the isentropic relations may be used over the expansion region.
over an expansion region we will get an increase in flow Mach number, decrease in pressure, decrease in density and decrease in temperature.
Starting from a geometrical analyze of the slight change in flow angle over one single Mach wave and assuming calorically perfect gas, the Prandtl-Meyer function is derived. The Prandtl-Meyer function can be used to obtain the downstream flow Mach number after a expansion region given the upstream Mach number and deflection angle.
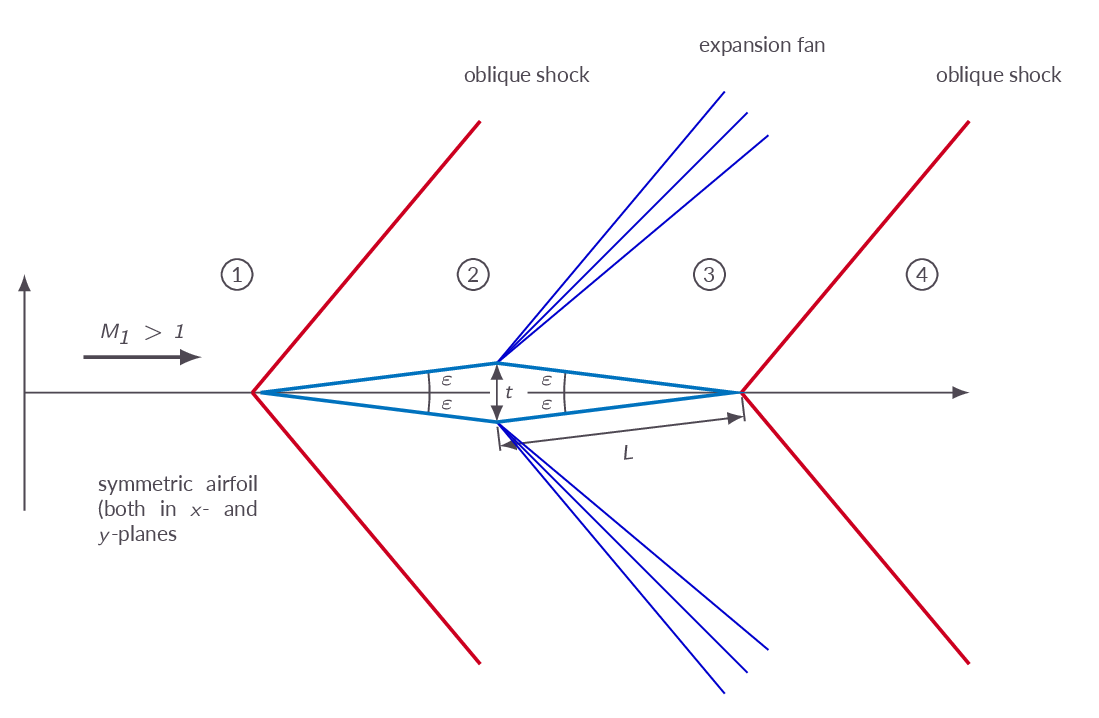
4.15 Shock-Expansion Theory
Shock expansion theory is nothing else but the analysis of flow situations including both shock waves and expansion waves. As an example the flow over a diamond wedge is analyzed and also the flow over a flat plate at an angle of attack. Using the oblique shock relations and the Prandtl-Meyer function we are able to obtain pressures on all surfaces of the diamond wedge and flat plate and thus lift and drag forces can be calculated.
Study Guide
The questions below are intended as a "study guide" and may be helpful when reading the text book.
Stationary Oblique Shock in Two-Dimensional Steady-State Inviscid Supersonic Flow
- How is the control volume theorem applied to the stationary oblique shock?
- How do the resulting equations differ from those of the stationary normal shock?
- How can you apply the formulas for a stationary normal shock to compute a stationary oblique shock? How can you use Table A.2 in the book for an oblique shock?
- How come that relations including total conditions derived for normal shocks must not be used for oblique shocks?
- What is a shock polar?
- What is the \(\theta-\beta-M\) relation?
- The oblique shock generated by a two-dimensional wedge in a supersonic steady-state flow can be either of the weak type or the strong type. What is the main difference between these two shock types and which type is usually seen in reality?
- How does the absolute Mach number change after a weak/strong stationary oblique shock?
- What happens if there is no possible solution? What is the reason for the no-solution situation?
- What kind of shock is obtained for a blunt body in supersonic flow?
- For a detached shock, indicate where you will find a normal shock, a strong oblique shock, a weak oblique shock, the sonic line.
- What is a slip line, and what conditions must be fulfilled across it? How can it be generated?
- Draw a schematic pressure-deflection diagram and explain how it is obtained.
- In steady-state 2D supersonic flow there are two types of shock reflection at solid walls. Name these two reflection types and describe the difference between them.
- When an oblique is reflected at a wall (regular reflection), will the reflection angle be specular? Justify your answer.
- What is a Mach wave and what is the angle of a Mach wave relative to the flow?
- In Formulas, Tables & Graphs, check formulas on pages (12-13). You should recognize the formulas for oblique shocks.
Stationary Expansion Wave in Two-Dimensional Steady-State Inviscid Supersonic Flow
- What is a centered simple wave, also known as a Prandtl-Meyer expansion?
- Is an expansion wave isentropic or non-isentropic?
- Describe how you can use the Prandtl-Meyer function to compute the change in Mach number due to a given flow deflection.
- In Formulas, Tables & Graphs, check formulas on pages (12-13). You should recognize the formulas for oblique shock and for Prandtl-Meyer expansion wave. In the book, look at Table A.5 to check how to use the Prandtl-Meyer function.
Shock-Expansion Theory
- Describe how oblique shocks and expansion fans may be combined to compute the steady-state inviscid supersonic flow around airfoils that consist of straight edges, e.g. the diamond-wedge airfoil or the flat plat airfoil. Explain also how and where slip lines may develop.
- Why do we always obtain a non-zero drag, even though the flow is inviscid?
