Chapter 5
Quasi-One-Dimensional Flow
Quasi-One-Dimensional Flow
Overview
Chapter 5 adds to the theory presented in Chapter 3 by extending the equations from on-dimensional flow to quasi one-dimensional flows. Quasi one dimensional implies that we still have variations of flow quantities in one direction only but we allow the cross section area of stream tubes to vary along the same direction as well. This means that we will be able to analyze axisymmetric channels with varying cross section areas such as for example convergent-divergent nozzles. One thing that is important to note is that for the equations to be valid the variation in cross section area has to be smooth.
Online Flow Calculator
Sections of the online flow calculator for compressible flow problems CFLOW related to this chapter:
- Section 1.: Gas Relations
- Section 2.: Total Flow Properties
- Section 3.: Normal Shock Relations
- Section 6.: Oblique Shock Relations
- Section 8.: Nozzle Flow
The CFLOW finite-volume quasi-1D solver can also be used to study the problems in this chapter.
Chapter Roadmap
Sections
5.2 Governing Equations
The governing equations for quasi one-dimensional flows are derived. The resulting continuity and energy equations are unchanged compared to the corresponding equations derived for one-dimensional flows in Chapter 3. In the momentum equation, however, we get a contribution from the pressure forces on the control volume perimeter surface (the surface aligned with the stream lines) that was not present in the momentum equation for one-dimensional flows. Moreover, the new term appears as an integral in the equation, which means that we need to rewrite the equations on differential form. This leads us to a momentum equation on a form known as the Euler equation.
$$ dp=-\rho udu $$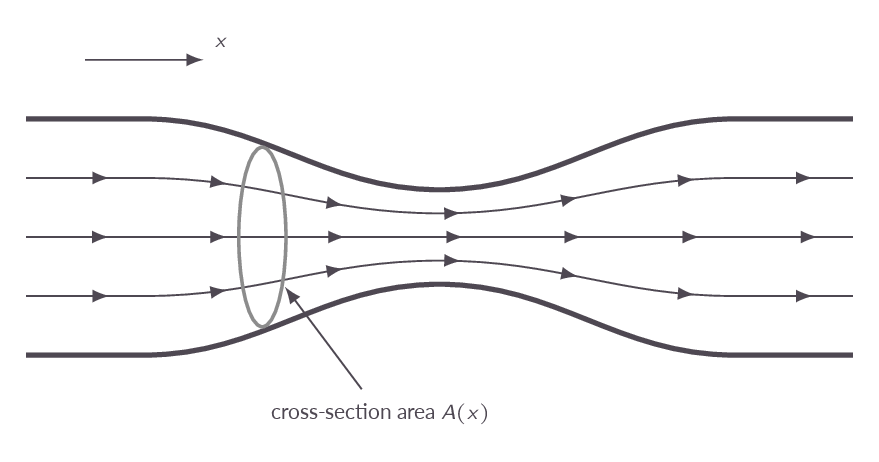
5.3 Area-Velocity Relation
Starting from the continuity equation, the momentum equation, and making an assumption of isentropic flow, the area-velocity relation is derived. This relation is an important contribution to the compressible flow engineering field since it describes gives us information on how to accelerate a flow to supersonic speeds.
$$ \frac{dA}{A}=(M^2-1)\frac{du}{u} $$5.4 Nozzles
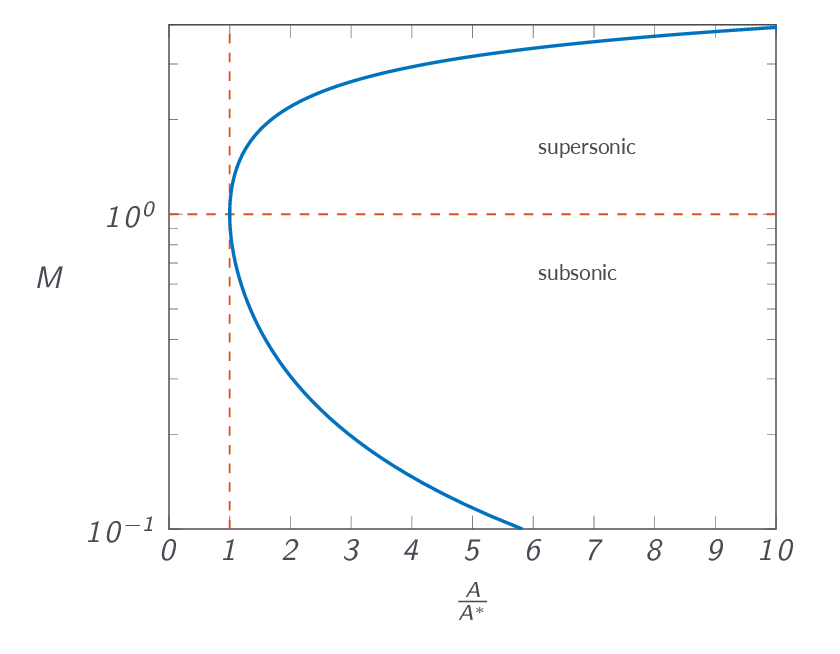
In this section another important relation is derived, namely the area-Mach number relation. The area-Mach number relation gives the ratio of local area to throat area as a function of Mach number (or the other way around). The area-Mach number relation is valid for isentropic flows (i.e. no shocks allowed) and calorically perfect gases.
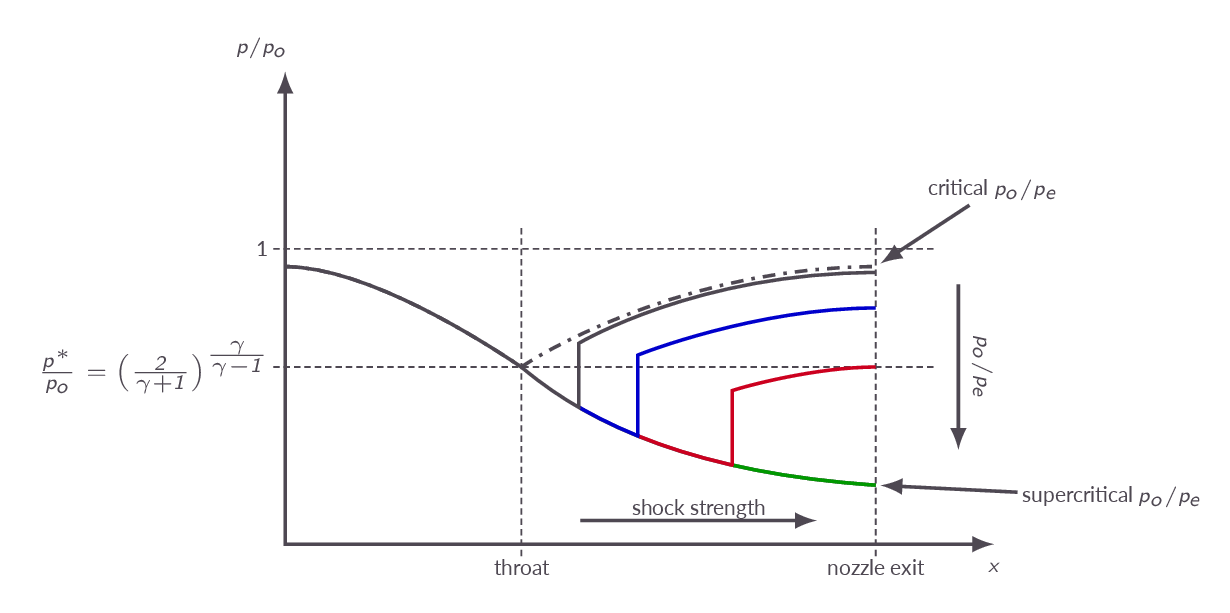
With the area distribution of a nozzle given we will be able to get the Mach number as function of \(x\) and thus also (using the isentropic relations) \(p/p_o\), \(T/T_o\), etc. It should be noted that there are a infinite number of possible scenarios with isentropic subsonic flow through the entire nozzle but only one possible solution where we get supersonic flow in the divergent part of the nozzle. The nozzle flow is highly dependent on the back pressure. If the back pressure is to high, we will get a normal shock at an axial location in the divergent part of the nozzle. Upstream of the normal shock, the flow will follow the isenttropic supersonic solution and on the downstream side we will get subsonic flow. The normal shock moves downstream the nozzle as the back pressure is reduced and for one specific back pressure we will have a normal shock standing at the nozzle exit plane. This means that we will have isentropic shock-free supersonic flow throughout the divergent part pf the nozzle. Reducing the back pressure further, results in overexpanded conditions leading to generation of oblique shocks at the nozzle exit going out from the nozzle. With further decrease of back pressure we may reach pressure matched conditions (flow without shocks or expansion waves) and if we continue to decrease the back pressure after that we will get formation of expansion waves at the nozzle exit. In the latter case the nozzle is said to be operating at underexpanded conditions.
A relation for calculation of the mass flow through a choked nozzle is derived.
$$ \dot{m}=\frac{p_o A^*}{\sqrt{T_o}}\sqrt{\frac{\gamma}{R}\left(\frac{2}{\gamma+1}\right)^{(\gamma+1)/(\gamma-1)}} $$

5.5 Diffusers
Diffuser flow is exemplified by describing the basic concepts of a supersonic wind tunnel. As a first example, supersonic flow coming from a convergent-divergent nozzle is going through a normal shock and then a simple diffuser. This setup gives a significant improvement compared to let the flow from the nozzle directly to the atmosphere. A system of oblique shocks in a diffuser section of a wind tunnel results in way better performance.
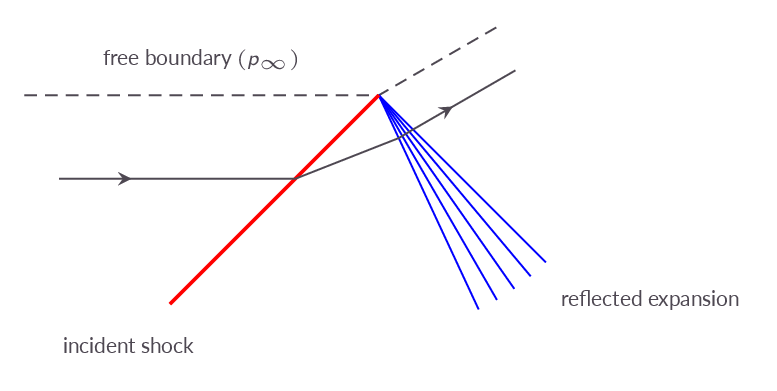
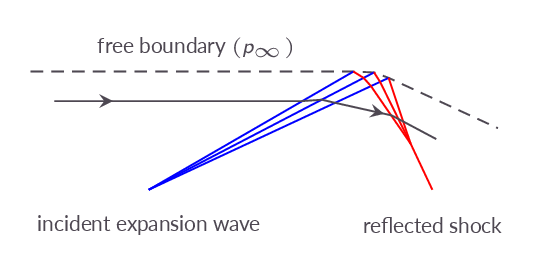
5.6 Wave Reflection from a Free Boundary
Waves emanating from non-perfectly expanded nozzles will reflect at the jet shear layer and the jet centerline resulting in a shock diamond pattern downstream of the nozzle exit. The shock diamond flow is not governed by the quasi one-dimensional theory but still included in this section since it is associated with supersonic nozzle flows.
Study Guide
The questions below are intended as a "study guide" and may be helpful when reading the text book.
- How do we apply the control volume theorems to this type of flow?
- How do the resulting equations differ from those of standard 1D flow?
- What further assumption do we need to derive the area-velocity relation?
- What are the implications of the area-velocity relation for quasi-one-dimensional flow?
- What additional assumptions do we need to derive the area-Mach relation?
- Check the shape of the area-Mach relation as given in Table A.1
- Describe the sub-critical flow in a converging-diverging nozzle, in terms of how we move along the area-Mach curve.
- Describe the critical flow in the same terms.
- What is meant by choked flow in a converging-diverging nozzle?
- Describe how the flow in a converging-diverging nozzle develops as we gradually increase the nozzle pressure ratio \(p_o/p_e\).
- What do we mean by an overexpanded nozzle flow?
- What do we mean by an underexpanded nozzle flow?
- What do we mean by a pressure-matched nozzle flow?
- Under what conditions will we get a normal shock standing at the exit plane of a convergent-divergent nozzle?
- Explain the consequence of free-boundary reflection for the external flow of a nozzle operating at overexpanded conditions.
- Assume a steady-state flow through a pipe with varying cross-section area. If the pipe has negligible heat transfer and wall friction and there are no shocks, then the flow is
- adiabatic
- isentropic
- isobaric (constant pressure)
- isenthalpic (constant enthalpy)
- Assume a steady-state flow in a convergent-divergent nozzle. Describe what characterizes the following operating conditions:
- Sub-critical nozzle flow
- Over-expanded nozzle flow
- Under-expanded nozzle flow
- Derive the area-velocity relation in quasi-1D flow starting from the mass conservation relation $$d(\rho uA)=0.,$$ Euler’s equation $$dp=-\rho udu,$$ and the definition of the speed of sound $$a^2=\left(\frac{\partial p}{\partial \rho}\right)_s$$
- In Formulas, Tables & Graphs, check formulas on pages (14-15). You should recognize the area-velocity and area- Mach relations, the choked mass flow relation and the equation giving the exit Mach number for cases with an internal normal shock.
