table of content

---

Unsteady Wave Motion

---

Overview

So far, we have only studied waves under steady state conditions, i.e. stationary normal shocks, expansion fans and Mach waves. In chapter 7 we will be introduced to unsteady waves. Chapter 7 starts with deriving relations for moving normal shocks then theory related to acoustic wave propagation is presented and finally something that is referred to as finite nonlinear waves is discussed. The shock tube is an application where all sorts of traveling waves are present. Due to the simplicity of the shock tube and the fact that the traveling waves may be treated as one-dimensional makes it a good application for analytical analysis and therefore the shock tube is used as an example throughout chapter 7. In the end of the chapter when all types of traveling waves present in the shock tube has been introduced, the shock tube relations are derived and discussed.

Online Flow Calculator

Sections of the online flow calculator for compressible flow problems CFLOW related to this chapter:

• Section 1: Gas Relations
• Section 2: Total Flow Properties
• Section 3: Normal Shock Relations
• Section 9: Unsteady Wave Motion
• Section 10: The Shock Tube

The CFLOW finite-volume quasi-1D solver can also be used to study the problems in this chapter.

Chapter Roadmap

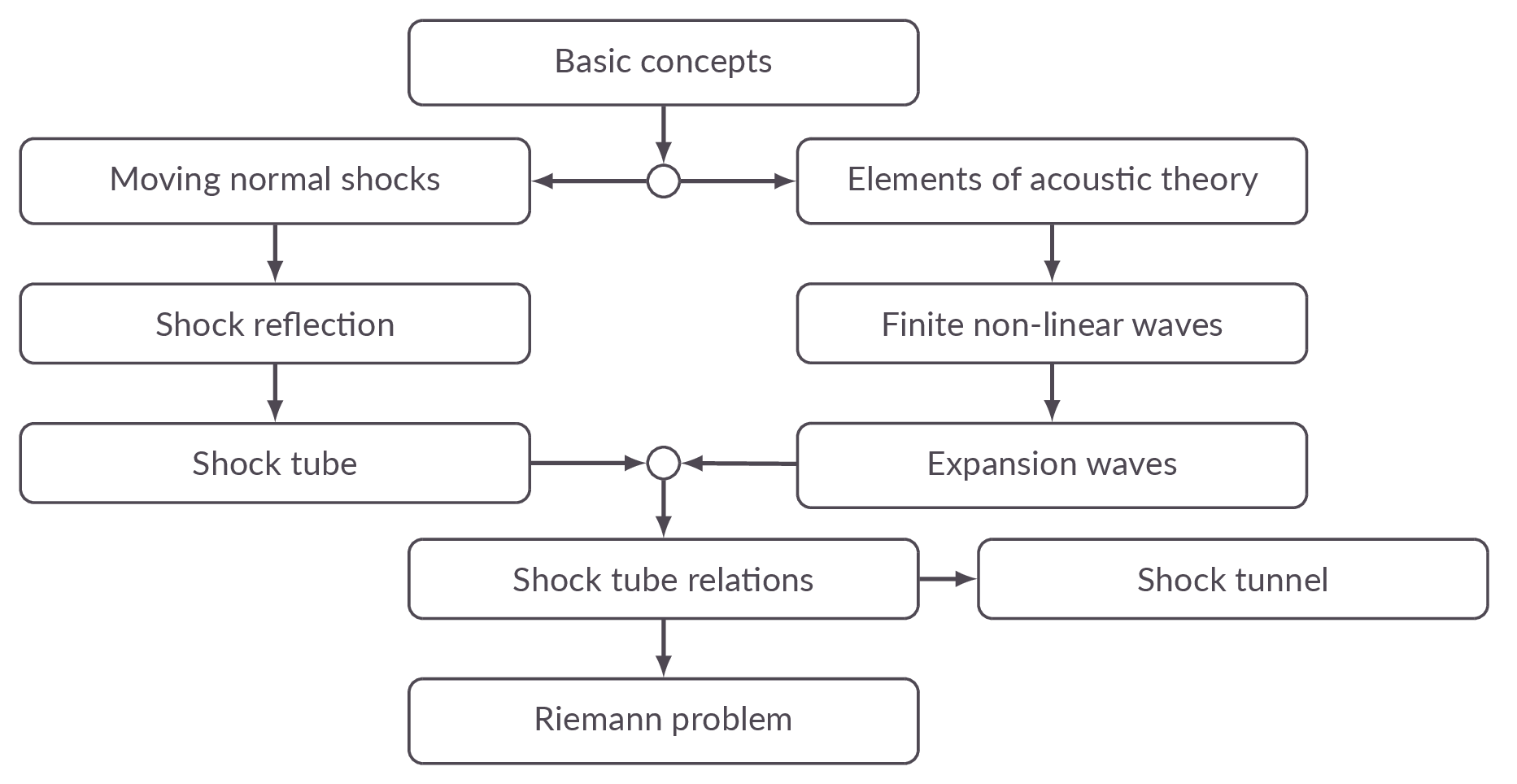
Sections

7.2 Moving Normal Shock Waves

The governing equations for a moving normal shock wave are presented. A normal shock moves with the velocity \(W\) in a stagnant fluid. In a frame of reference following the normal shock we will see a fluid motion ahead of the shock with velocity \(W\) relative to the shock and the velocity of the fluid behind the wave (relative to the wave) will be \((W-u_p)\), where \(u_p\) is the induced velocity. With this in mind, the governing equations are easily obtained from the normal shock equations presented in Chapter 3.

$$\rho_1 W = \rho_2(W-u_p)$$ $$p_1+\rho_1 W^2 = p_2 +\rho_2(W-u_p)^2$$ $$h_1+\frac{W^2}{2} = h_2 + \frac{(W+u_p)^2}{2} $$

It is shown that the Hugoniot equation can be derived directly from these relations which implies that the thermodynamic relations are the same in the new frame of reference.

Expressions for calculation of the temperature and density ratios over the shock wave are derived. The expressions are based on the pressure ratio over the shock wave (the corresponding relations for stationary normal shocks presented in Chapter 3 where all based on the freestream Mach number ahead of the shock).

An expression for the calculation of the induced flow velocity \(u_p\) is derived. Again the relation is based on the pressure ratio over the moving shock. It turns out that if the shock becomes infinitely strong \(p_2/p_1\rightarrow\infty\), the induced Mach number approaches a finite value

$$\lim_{\frac{p_2}{p_1}\rightarrow \infty} M_p\rightarrow \sqrt{\frac{2}{\gamma(\gamma-1)}}$$

For air with \(\gamma=1.4\), the limiting value is 1.89. The fact that there is a limit to how high Mach number that can be induced by the moving shock wave is interesting as such but the example above also shows that the limiting value is a high supersonic value.

7.3 Reflected Shock Wave

Shock wave reflection is exemplified by events in the shock tube application. When the incident shock wave, generated when the diaphragm in the shock tube separating the two flow states bursts, approaches the right wall of the shock tube, the fluid behind the shock wave has a velocity relative to the wall equal to the induced flow velocity \(u_p\). Of course the flow can not go through the wall and therefore a shock propagating in the opposite direction is generated at the instant when the incident shock reaches the wall. The reflected shock is set up such that it brings the fluid behind it to rest and thus the fluid near the wall is standing still.

The governing equations for the reflected shock are presented

$$\rho_2 (W_r+u_p)=\rho_5 W_r$$ $$p_2+\rho_2(W_r+u_p)^2=p_5+\rho_5 W_r^2$$ $$h_2+\frac{1}{2}(W_r+u_p)^2=h_5+\frac{1}{2}W_r^2$$

A relation between the Mach number of the reflected shock and the Mach number of the incident shock is presented at the end of the section. The derivation is left for the reader to do. Since the derivation is a bit tricky it is provided in pdf format in the document archive at the bottom of this page.

$$\frac{M_r}{M_r^2-1}=\frac{M_s}{M_s^2-1}\sqrt{1+\frac{2(\gamma-1)}{(\gamma+1)^2}(M_s^2-1)\left(\gamma+\frac{1}{M_s^2}\right)}$$

7.4 Physical Picture of Wave Propagation

Wave propagation in one dimension is discussed as an introduction to the sections to follow. The concept finite wave is introduced.

7.5 Elements of Acoustic Theory

Propagation of acoustic waves are described as a natural part of the wave propagation section. An approximate equation governing the propagation of acoustic waves is derived using linearization. The starting point is the governing equations on differential form derived in Chapter 6. It is shown that in order to fulfill the wave equation, the waves must propagate with a constant velocity namely the speed of sound in the fluid in which the wave propagates.

Acoustic waves summarized:

• \(\Delta \rho\), \(\Delta u\), etc - very small
• All parts of the wave propagate with the same velocity \(a_\infty\)
• The wave shape stays the same
• The flow is governed by linear relations

7.6 Finite (Nonlinear) Waves

The discussion of wave propagation is continued with cases where the perturbations are not necessarily small, as was the case for the acoustic waves. Such waves, with significant or even large perturbations is what the author refer to as finite waves. For these finite waves nonlinearities may be significant and thus the linear relations obtained for the acoustic waves will not be adequate to use. Equations governing the propagation of finite waves are derived - again starting from the flow equations on differential form first presented in Chapter 6.

Analyzing the equations, it is observed that for waves moving along specific paths, the partial differential equations can be reduced to ordinary differential equations. These paths are referred to as characteristic lines and the technique introduced is the basis for the method of characteristics, which is of great importance for compressible flow analysis. From the characteristic lines, the Riemann invariants are obtained and it is showed how the Riemann invariants can be used for a calorically perfect gas to calculate the flow velocity and speed of sound in a location.

Finite nonlinear waves summarized:

• \(\Delta \rho\), \(\Delta u\), etc - can be large
• Each local part of the wave propagates at the local velocity (\(u+a\))
• The wave shape changes with time
• The flow is governed by non-linear relations

7.7 Incident and Reflected Expansion Waves

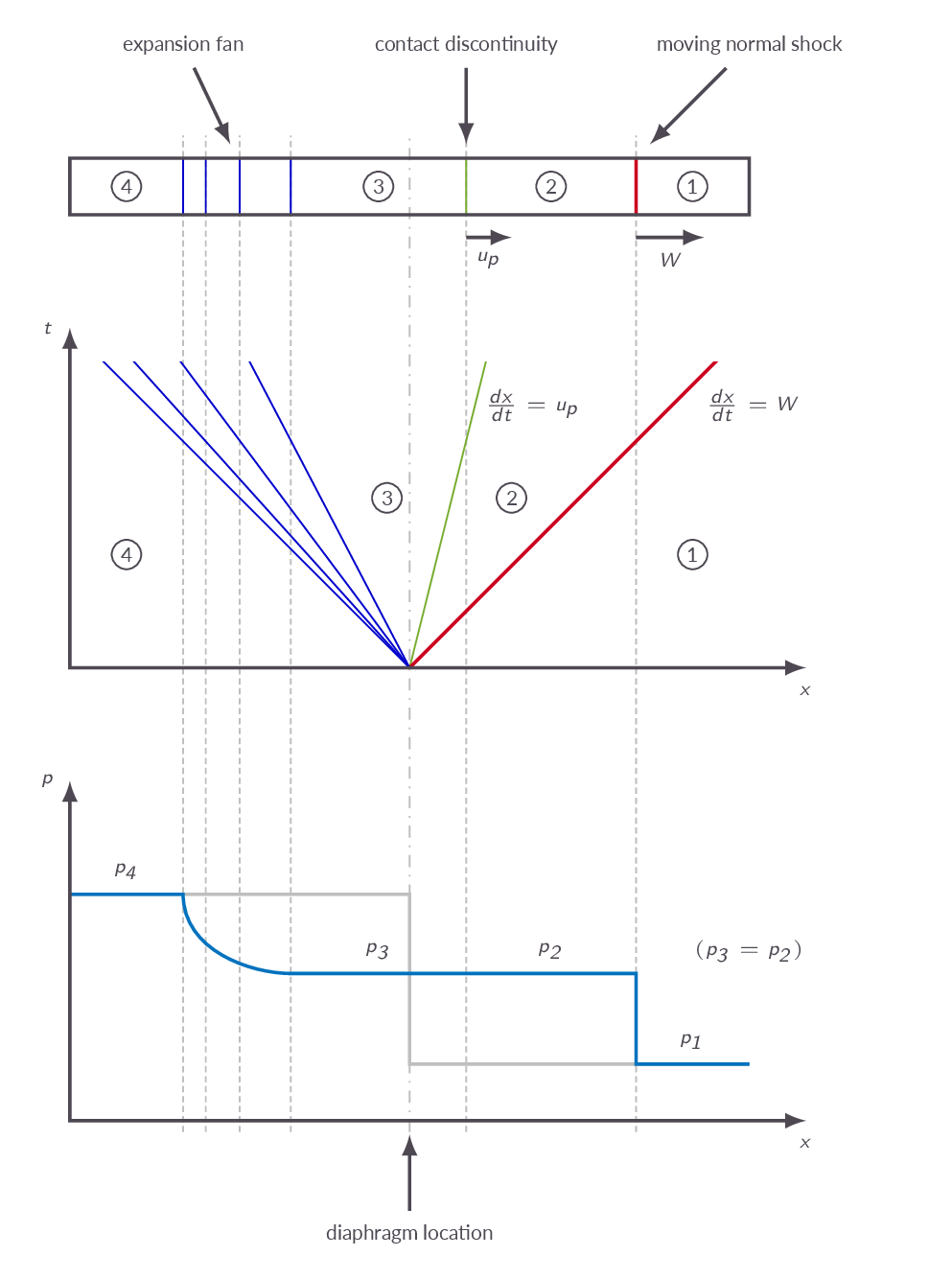
Again, the shock tube is used for illustration of traveling waves. In this section we sill learn how to analyze the expansion wave going to the left in the shock tube. The framework set up in the previous section based on characteristics and Riemann invariants is used to derive expressions relating the flow state into which the expansion wave is propagating (4) to the region behind the expansion region (3). Since both region 3 and 4 are regions with constant flow properties it can be shown that

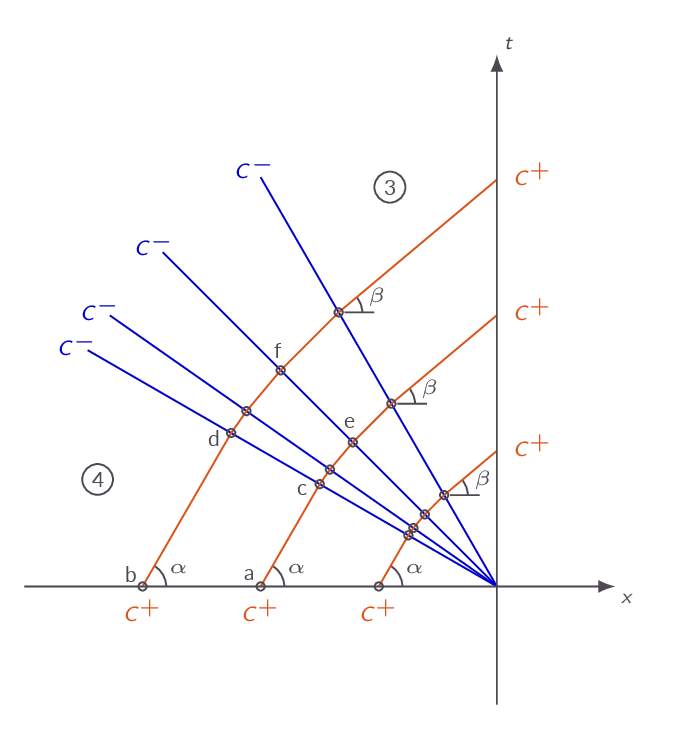
constant flow properties in region 4:

$$J^+_a=J^+_b$$

\(J^+\) invariants constant along \(C^+\) characteristics:

$$J^+_a=J^+_c=J^+_e$$ $$J^+_b=J^+_d=J^+_f$$

since \(J^+_a=J^+_b\) this also implies \(J^+_e=J^+_f\)

\(J^-\) invariants constant along \(C^-\) characteristics:

$$J^-_c=J^-_d$$ $$J^-_e=J^-_f$$

$$u_e=\frac{1}{2}(J^+_e+J^-_e),\ u_f=\frac{1}{2}(J^+_f+J^-_f),\ \Rightarrow u_e=u_f$$

$$a_e=\frac{\gamma-1}{4}(J^+_e-J^-_e),\ a_f=\frac{\gamma-1}{4}(J^+_f-J^-_f),\ \Rightarrow\ a_e=a_f$$

• The start and end conditions are the same for all \(C^+\) lines
• \(J^+\) invariants have the same value for all \(C^+\) characteristics
• \(C^-\) characteristics are straight lines in \(xt\)-space
• Simple expansion waves centered at \((x,t)=(0,0)\)

7.8 Shock Tube Relations

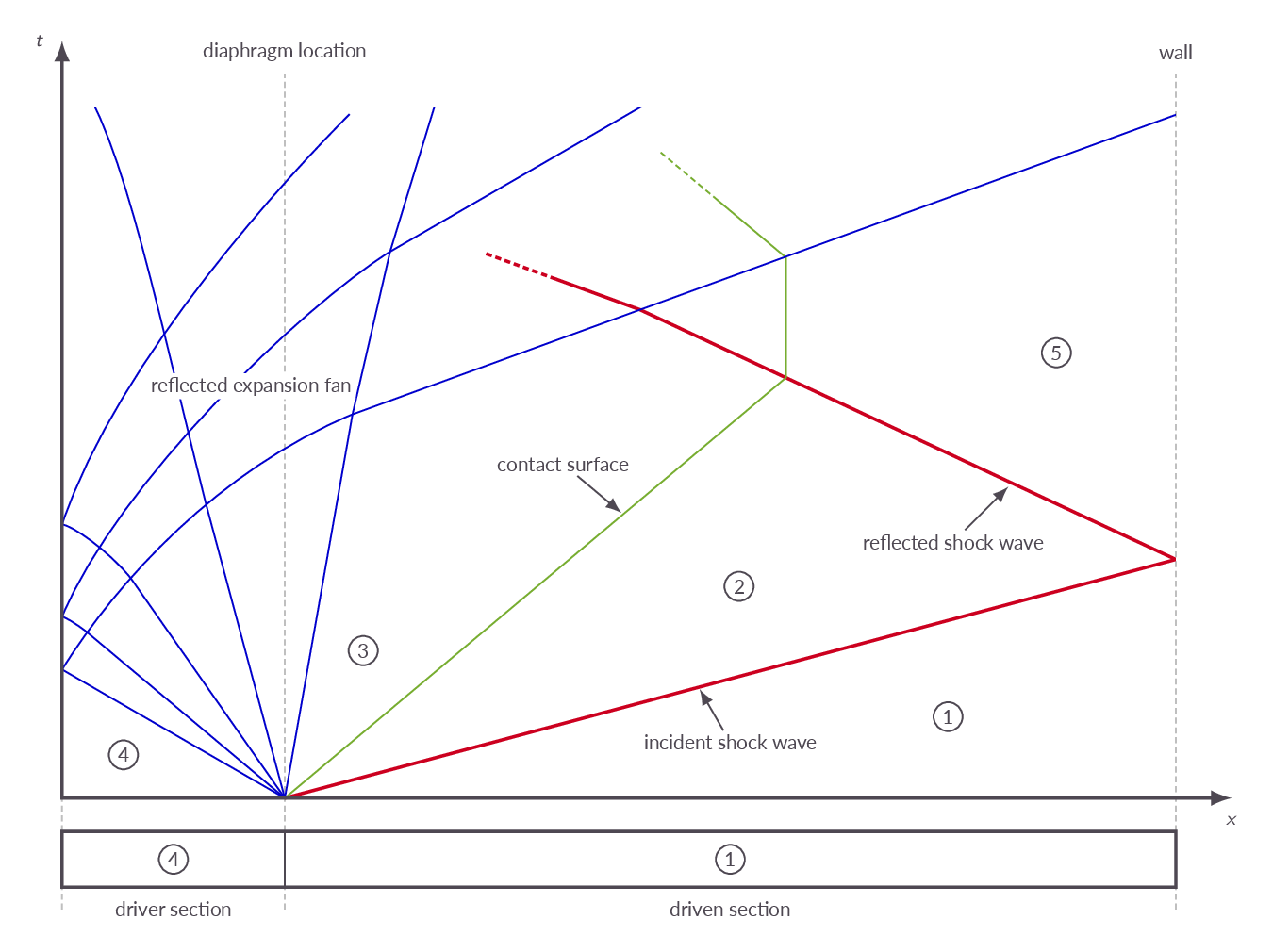
The shock tube problem is now completely defined since we can analyze all waves in the system. Combining the moving shock wave equations with the expansion region relations derived in the previous section it is now possible to derive an expression for the pressure ratio \(p_4/p_1\), i.e. the initial states in the shock tube.

$$\frac{p_4}{p_1}=\frac{p_2}{p_1}\left\{ 1 -\frac{(\gamma_4-1)(a_1/a_4)(p_2/p_1-1)}{\sqrt{2\gamma_1\left[2\gamma_1+(\gamma_1+1)(p_2/p_1-1)\right]}}\right\}^{-2\gamma_4/(\gamma_4-1)}$$

• \(p_2/p_1\) as implicit function of \(p_4/p_1\)
• for a given \(p_4/p_1\), \(p_2/p_1\) will increase with decreased \(a_1/a_4\)

7.9 Finite Compression Waves

With finite expansion waves covered in the previous section, finite compression waves are now discussed. In contrast to the expansion region that always spread in space over time the individual waves in the compression region will approach each other over time and the compression region will coalesce into a shock wave.

---

Study Guide

The questions below are intended as a "study guide" and may be helpful when reading the text book.

Moving Normal Shocks

Finite Non-Linear Waves

The Shock Tube

Acoustic Theory

---

Videos