table of content

---

Differential Conservation Equations for Inviscid Flows

---

Overview

Chapter 6 is devoted to the governing equations for compressible flows on differential form, i.e. it is a chapter very much like Chapter 2.

Chapter Roadmap

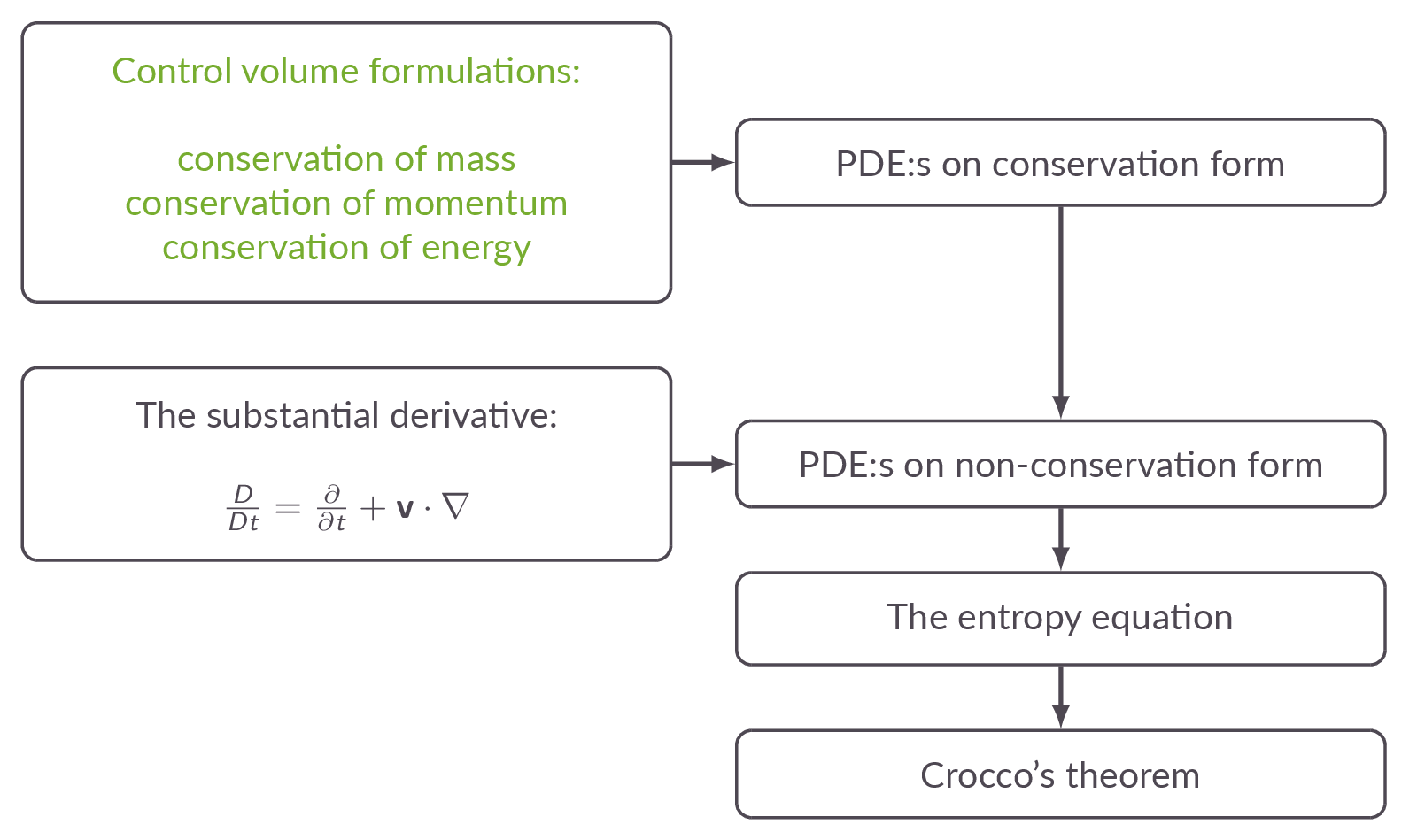
Sections

6.2 Differential Equations in Conservation Form

In this section the continuity, momentum, and energy equations on differential conservation form are derived. The starting point for the derivation is the integral form of the equations obtained in Chapter 2. The new set of equations constitutes a framework that can be applied and evaluated in any point of a three-dimensional inviscid flow.

$$\frac{\partial \rho}{\partial t} + \nabla \cdot(\rho{\mathbf{v}})=0$$ $$\frac{\partial}{\partial t}(\rho{\mathbf{v}}) + \nabla \cdot(\rho{\mathbf{vv}})+\nabla p = \rho{\mathbf{f}}$$ $$\frac{\partial}{\partial t}(\rho e_{o}) + \nabla \cdot(\rho h_{o}{\mathbf{v}}) = \rho({\mathbf{f}}\cdot{\mathbf{v}})$$

The Substantial Derivative

In this section the substantial derivative is introduced

$$\frac{D}{Dt}=\frac{\partial}{\partial t}+{\mathbf{v}}\cdot \nabla$$

... the time rate of change of any quantity associated with a particular moving fluid element is given by the substantial derivative ...

... the properties of the fluid element are changing as it moves past a point in a flow because the flowfield itself may be fluctuating with time (the local derivative) and because the fluid element is simply on its way to another point in the flowfield where the properties are different (the convective derivative) ...

Differential Equations in Nonconservation Form

The differential equations derived in this section are applicable when one wants to follow the development of a specific fluid element in space and time. A new set of governing equations are derived. The continutiy equation reads

$$\frac{D\rho}{Dt}+\rho(\nabla\cdot{\mathbf{v}})=0$$

... the mass of a fluid element made up of a fixed set of particles (molecules or atoms) is constant as the fluid element moves through space ...

The momentum equation:

$$\frac{D{\mathbf{v}}}{Dt}+\frac{1}{\rho}\nabla p={\mathbf{f}}$$

The energy equation:

$$\frac{De}{Dt}+\frac{p}{\rho}(\nabla\cdot{\mathbf{v}})=\dot{q}$$

In the last few pages of this section alternative formulations of the energy equation are derived. The total entropy formulation of the energy equation is analysed and discussed in some detail.

$$\frac{Dh_{o}}{Dt}=\frac{1}{\rho}\frac{\partial p}{\partial t}+\dot{q}+{\mathbf{f}}\cdot{\mathbf{v}}$$

As can be seen in the equation above, the total enthalpy of a moving fluid element in an inviscid flow can change due to

• unsteady flow: \(\partial p/\partial t \ne 0\)
• heat transfer: \(\dot{q} \ne 0\)
• body forces: \({\mathbf{f}}\cdot{\mathbf{v}} \ne 0\)

Adiabatic flow and without body forces gives:

$$\frac{Dh_{o}}{Dt}=\frac{1}{\rho}\frac{\partial p}{\partial t}$$

For steady-state adiabatic flow without body forces we get

$$\frac{Dh_{o}}{Dt}=0$$

\(h_{o}\) is constant along streamlines!

It should be noted that the equations derived in this sections are not non-conservative as such, the term non-conservative refers to properties of the equations when used for the development of CFD tools.

The Entropy Equation

From the first and second law of thermodynamics we have

$$\frac{De}{Dt}=T\frac{Ds}{Dt}-p\frac{D}{Dt}\left(\frac{1}{\rho}\right)$$

which is called the entropy equation. By comparing with the energy equation one can see that if the flow is adiabatic we get

$$\frac{Ds}{Dt}=0$$

which means that entropy is constant for moving fluid element. Furthermore, if the flow is steady we have

$$\frac{Ds}{Dt}=\frac{\partial s}{\partial t}+({\mathbf{v}}\cdot\nabla)s=({\mathbf{v}}\cdot\nabla)s=0$$

which implies that entropy is constant along streamlines.

Crocco's Theorem

... Crocco's theorem is a relation between gradients of total enthalpy, gradients of entropy, and flow rotation ...

$$T \nabla s=\nabla h_{o}+\frac{\partial {\mathbf{v}}}{\partial t}-{\mathbf{v}}\times(\nabla\times{\mathbf{v}})$$

Note: \(\nabla\times{\mathbf{v}}\) is the vorticity of the fluid

... when a steady flow field has gradients of total enthalpy and/or entropy Crocco's theorem dramatically shows that it is rotational ...

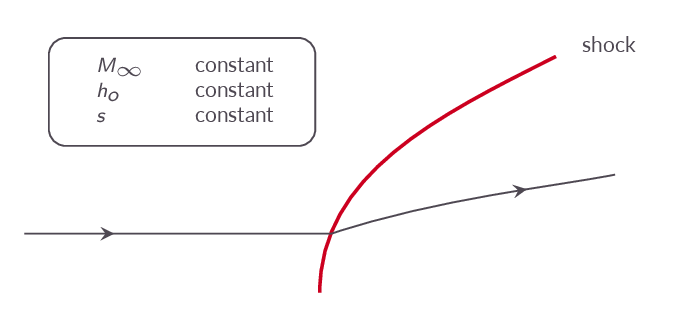
• Entropy change over shock
• \(s\) is constant upstream of shock
• jump in \(s\) across shock depends on local shock angle
• \(s\) will vary from streamline to streamline downstream of shock
• \(\nabla s\neq 0\) downstream of shock
• Total enthalpy upstream of shock
• \(h_{o}\) is constant along streamlines
• \(h_{o}\) is uniform
• Total enthalpy downstream of shock
• \(h_{o}\) is uniform
• \({\mathbf{v}}\times(\nabla\times{\mathbf{v}})\neq 0\) downstream of a curved shock
• the rotation \(\nabla\times{\mathbf{v}}\neq 0\) downstream of a curved shock

Explains why it is difficult to solve such problems by analytic means!

---

Study Guide

The questions below are intended as a "study guide" and may be helpful when reading the text book.